Introdução a dados de áudio

Por natureza, uma onda sonora é um sinal contínuo, o que significa que contém um número infinito de valores de sinal em um determinado tempo. Isso traz problemas para dispositivos digitais que esperam arrays finitos. Para ser processada, armazenada e transmitida por dispositivos digitais, a onda sonora contínua precisa ser convertida em uma série de valores discretos, conhecidos como representação digital.

Se você olhar para qualquer dataset de áudio, encontrará arquivos digitais com trechos de som, como narração de texto ou música. Você pode encontrar diferentes formatos de arquivo, como .wav (Waveform Audio File), .flac (Free Lossless Audio Codec) e .mp3 (MPEG-1 Audio Layer 3). Esses formatos diferem principalmente na forma como comprimem a representação digital do sinal de áudio.

Vamos dar uma olhada em como saímos de um sinal contínuo para essa representação. O sinal analógico é primeiro capturado por um microfone, que converte as ondas sonoras em um sinal elétrico. O sinal elétrico é então digitalizado por um Conversor Analógico-Digital para obter a representação digital por meio da amostragem.

Amostragem e taxa de amostragem

Amostragem (sampling) é o processo de medir o valor de um sinal contínuo em etapas (amostras) que possuem o mesmo tempo. A forma da onda que foi amostrada é discreta, pois contém um número finito dos valores do sinal em intervalos uniformes.

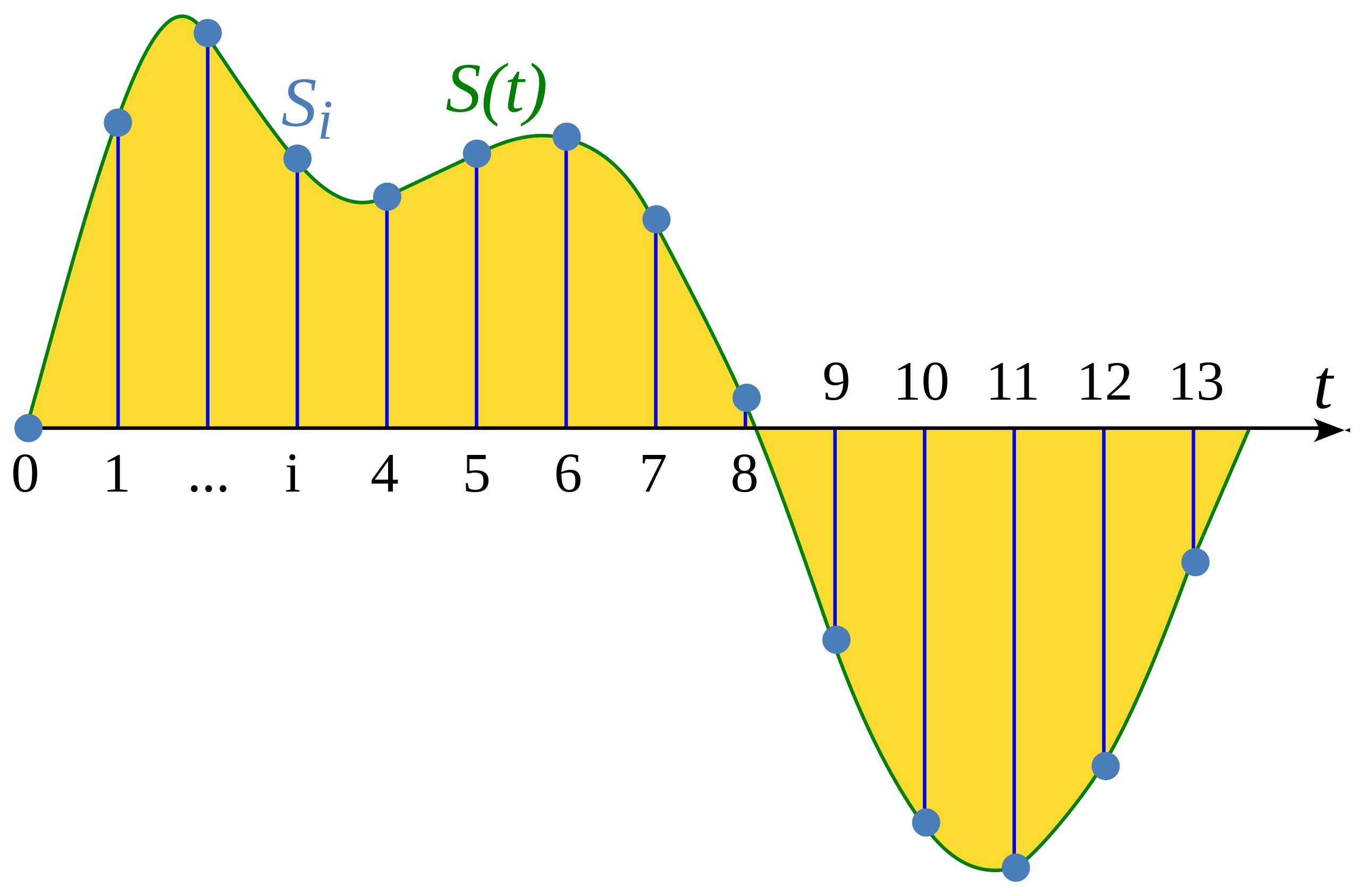
Ilustração deste artigo da Wikipedia: Amostragem (processamento de sinal)

A taxa de amostragem (também chamada de frequência de amostragem, sampling rate ou sampling frequency) é o número de amostras feitas em um segundo e é medida em hertz (Hz). Para você ter ideia, áudio com qualidade de CD tem uma taxa de amostragem de 44.100 Hz, o que significa que as amostras são feitas 44.100 vezes por segundo. Para comparação, o áudio de alta resolução tem uma taxa de amostragem de 192.000 Hz ou 192 kHz. Uma taxa de amostragem comum usada no treinamento de modelos de fala é de 16.000 Hz ou 16 kHz.

A escolha da taxa de amostragem determina, principalmente, a maior frequência que pode ser capturada do sinal. Isso também é conhecido como o limite de Nyquist e é exatamente a metade da taxa de amostragem. As frequências audíveis na fala humana estão abaixo de 8 kHz e, portanto, amostrar a fala a 16 kHz é suficiente. Usar uma taxa de amostragem mais alta não capturará mais informações e apenas leva a um aumento no custo computacional de processar tais arquivos. Por outro lado, amostrar áudio em uma taxa de amostragem muito baixa resultará em perda de informação. A fala amostrada a 8 kHz soará abafada, pois as frequências mais altas não podem ser capturadas nessa taxa.

É importante garantir que todos os exemplos de áudio no seu dataset tenham a mesma taxa de amostragem ao trabalhar em qualquer processamento de áudio. Se você planeja usar dados de áudio personalizados para ajustar um modelo pré-treinado, a taxa de amostragem dos seus dados deve corresponder à taxa de amostragem dos dados em que o modelo foi pré-treinado. A taxa de amostragem determina o intervalo de tempo entre amostras de áudio sucessivas, o que impacta a resolução temporal dos dados de áudio. Considere um exemplo: um som de 5 segundos a uma taxa de amostragem de 16.000 Hz será representado como uma série de 80.000 valores (16.000 x 5), enquanto o mesmo som de 5 segundos a uma taxa de amostragem de 8.000 Hz será representado como uma série de 40.000 valores. Modelos Transformers que resolvem tarefas de áudio tratam exemplos como sequências e dependem de mecanismos de atenção para aprender áudio ou representações multimodais. Como as sequências são diferentes para exemplos de áudio em diferentes taxas de amostragem, será desafiador para os modelos generalizarem entre taxas de amostragem. Reamostragem (Resampling) é o processo de fazer as taxas de amostragem se igualarem, e faz parte do pré-processamento dos dados de áudio.

Amplitude e profundidade de bits (bit depth)

Enquanto a taxa de amostragem diz com que frequência as amostras são feitas, o que exatamente são os valores em cada amostra?

O som é feito por mudanças na pressão do ar em frequências audíveis para humanos. A amplitude de um som descreve o nível de pressão sonora em um dado momento e é medida em decibéis (dB). Percebemos a amplitude como volume. Para lhe dar um exemplo, uma voz falando normalmente está abaixo de 60 dB, e um show de rock pode estar em torno de 125 dB, forçando os limites da audição humana.

No áudio digital, cada amostra do áudio é o valor da amplitude da onda sonora em um ponto no tempo. A profundidade de bits (bit depth) da amostra determina o quão preciso esse valor pode ser. Quanto maior a profundidade de bits, mais fiel será a representação digital da onda sonora contínua original.

As profundidades de bit de áudio mais comuns são 16 bits e 24 bits. Cada uma representa o número máximo de valores distintos que podem ser registrados em cada amostra: 65.536 valores para áudio de 16 bits, impressionantes 16.777.216 valores para áudio de 24 bits. Devido ao fato que essa quantização do valor contínuo para o discreto envolve arredondamento, o processo de amostragem causa ruído. Quanto maior a profundidade de bits, menor esse ruído de quantização. Na prática, o ruído de quantização do áudio de 16 bits já é pequeno o suficiente para ser inaudível, e usar profundidades de bits maiores geralmente não é necessário.

Você também pode encontrar áudio de 32 bits. Isso armazena as amostras como valores de ponto flutuante (decimal), enquanto o áudio de 16 bits e 24 bits usa amostras inteiras. A precisão de um valor de ponto flutuante de 32 bits é de 24 bits, dando-lhe a mesma profundidade de bits que o áudio de 24 bits. Amostras de áudio de ponto flutuante são esperadas para estar dentro do intervalo [-1.0, 1.0]. Como os modelos de machine learning trabalham naturalmente com dados de ponto flutuante, o áudio deve primeiro ser convertido para o formato de ponto flutuante antes de poder ser usado para treinar o modelo. Veremos como fazer isso na próxima seção sobre Pré-processamento.

Assim como com sinais de áudio contínuos, a amplitude do áudio digital é tipicamente expressa em decibéis (dB). Como a audição humana é logarítmica por natureza — nossos ouvidos são mais sensíveis a pequenas flutuações em sons silenciosos do que em sons altos — a intensidade de um som é mais fácil de interpretar se as amplitudes estiverem em decibéis, que também são logarítmicos. A escala de decibéis para áudio do mundo real começa em 0 dB, que representa o som mais baixo possível que os humanos podem ouvir, e sons mais altos têm valores maiores. No entanto, para sinais de áudio digitais, 0 dB é a amplitude mais alta possível, enquanto todas as outras amplitudes são negativas. Como uma regra rápida: a cada -6 dB é uma redução pela metade da amplitude, e qualquer coisa abaixo de -60 dB geralmente é inaudível a menos que você realmente aumente o volume.

Áudio como uma forma de onda

Você já pode ter visto sons visualizados como uma forma de onda, que traça os valores das amostras ao longo do tempo e ilustra as mudanças na amplitude do som. Isso também é conhecido como a representação do domínio do tempo do som.

Esse tipo de visualização é útil para identificar características específicas do sinal de áudio, como o momento de eventos sonoros individuais, o volume geral do sinal e quaisquer irregularidades ou ruídos presentes no áudio.

Para traçar a forma de onda de um sinal de áudio, podemos usar uma biblioteca Python chamada librosa:

pip install librosa

Vamos pegar um exemplo de som chamado “trompete” que vem com a biblioteca:

import librosa

array, sampling_rate = librosa.load(librosa.ex("trumpet"))

O exemplo é carregado como uma tupla contendo uma sequencia temporal de áudio (aqui chamamos de array) e a taxa de amostragem (sampling_rate). Vamos dar uma olhada na forma de onda deste som usando a função waveshow() da librosa:

import matplotlib.pyplot as plt
import librosa.display

plt.figure().set_figwidth(12)
librosa.display.waveshow(array, sr=sampling_rate)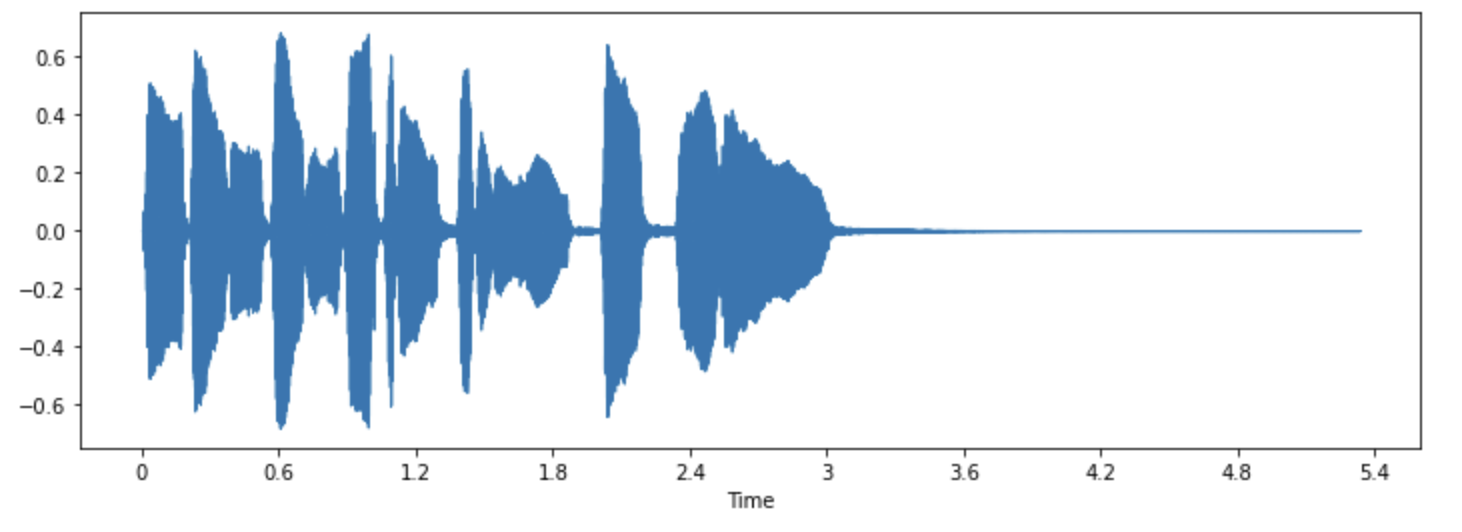

Isso coloca a amplitude do sinal no eixo y e o tempo ao longo do eixo x. Em outras palavras, cada ponto corresponde a um único valor de amostra que foi feito quando este som foi amostrado. Também observe que a librosa já retorna o áudio como valores de ponto flutuante e que os valores de amplitude estão de fato dentro do intervalo [-1,0, 1,0].

Visualizar o áudio junto com ouvi-lo pode ser uma ferramenta útil para entender os dados com os quais você está trabalhando. Você pode ver a forma do sinal, observar padrões, aprender a identificar ruídos ou distorção. Se você pré-processar dados de alguma forma, como normalização, reamostragem ou filtragem, você pode confirmar visualmente que as etapas de pré-processamento foram aplicadas conforme esperado. Após treinar um modelo, você também pode visualizar amostras onde ocorrem erros (por exemplo, em tarefa de classificação de áudio) para fazer o debug do problema.

O espectro de frequência

Outra maneira de visualizar dados de áudio é plotar o espectro de frequência de um sinal de áudio, também conhecido como a representação do domínio da frequência. O espectro é calculado usando a transformada de Fourier discreta ou DFT. Ele descreve as frequências individuais que compõem o sinal e quão fortes elas são.

Vamos plotar o espectro de frequência para o mesmo som de trompete, fazendo a DFT usando a função rfft() do numpy. Embora seja possível plotar o espectro de todo o som, é mais útil olhar para uma pequena região em vez disso. Aqui vamos fazer a DFT sobre as primeiras 4096 amostras, que é aproximadamente o comprimento da primeira nota sendo tocada:

import numpy as np

dft_input = array[:4096]

# calcula a DFT
window = np.hanning(len(dft_input))
windowed_input = dft_input * window
dft = np.fft.rfft(windowed_input)

# obtém as amplitude do espectro, em decibeis
amplitude = np.abs(dft)
amplitude_db = librosa.amplitude_to_db(amplitude, ref=np.max)

# obtém a frquency bins (faixas de frequencia)
frequency = librosa.fft_frequencies(sr=sampling_rate, n_fft=len(dft_input))

plt.figure().set_figwidth(12)
plt.plot(frequency, amplitude_db)
plt.xlabel("Frequency (Hz)")
plt.ylabel("Amplitude (dB)")
plt.xscale("log")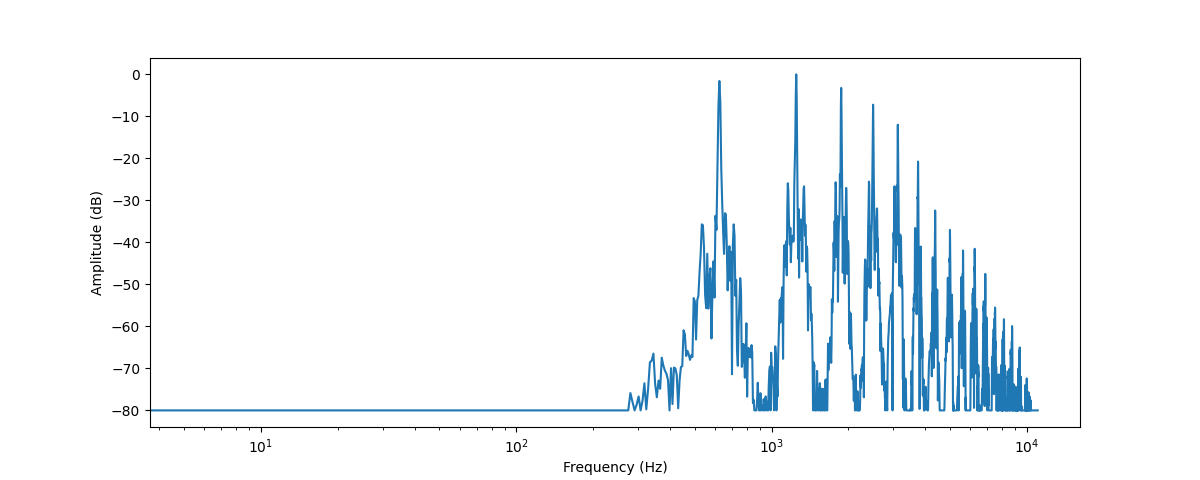

Isso mostra um gráfico com a força de várias frequências que estão presentes neste trecho de áudio. Os valores da frequência estão no eixo x, geralmente plotados em uma escala logarítmica, enquanto suas amplitudes estão no eixo y.

O espectro de frequência que plotamos mostra vários picos. Esses picos correspondem aos harmônicos da nota que está sendo tocada, com os harmônicos superiores sendo mais silenciosos. Como o primeiro pico está em torno de 620 Hz, este é o espectro de frequência de uma nota E♭ (Mi bemol).

O resultado da DFT é um array de números complexos, compostos de componentes reais e imaginários. Obtendo a magnitude (valor absoluto, sem sinal) com np.abs(dft), extraímos as informação de amplitude do espectrograma. O ângulo entre os componentes reais e imaginários fornece o chamado espectro de fase, mas isso é frequentemente descartado em aplicações de machine learning.

Você usou librosa.amplitude_to_db() para converter os valores de amplitude para a escala de decibéis, facilitando a visualização dos mínimos detalhes no espectro. Às vezes, as pessoas usam o espectro de potência, que mede a energia em vez da amplitude; isso é simplesmente um espectro com os valores de amplitude ao quadrado.

O espectro de frequência de um sinal de áudio contém exatamente as mesmas informações que sua forma de onda — são simplesmente duas maneiras diferentes de olhar para os mesmos dados (no caso, as primeiras 4096 amostras do som de trompete). Enquanto a forma de onda traça a amplitude do sinal de áudio ao longo do tempo, o espectro visualiza as amplitudes de cada frequência em um ponto fixo no tempo.

Espectrograma

E se quisermos ver como as frequências em um sinal de áudio mudam? O trompete toca várias notas e todas elas têm frequências diferentes. O problema é que o espectro mostra apenas “uma foto” das frequências em um dado instante. A solução é fazer várias DFTs, cada uma cobrindo apenas uma pequena fatia de tempo, e empilhar os espectros resultantes formando um espectrograma.

Um espectrograma mostra o conteúdo da frequência de um sinal de áudio à ao longo do tempo. Ele permite que você veja tempo, frequência e amplitude tudo em um único gráfico. O algoritmo que realiza esse cálculo é o STFT (Short Time Fourier Transform) ou Transformada de Fourier de Tempo Curto.

O espectrograma é uma das ferramentas de áudio mais informativas disponíveis para você. Por exemplo, ao trabalhar com uma gravação de música, você pode ver os vários instrumentos e faixas vocais e como eles contribuem para o som geral. Na fala, você pode identificar diferentes sons de vogais, pois cada vogal é caracterizada por frequências particulares.

Vamos plotar um espectrograma para o mesmo som de trompete, usando as funções stft() e specshow() da librosa:

import numpy as np

D = librosa.stft(array)
S_db = librosa.amplitude_to_db(np.abs(D), ref=np.max)

plt.figure().set_figwidth(12)
librosa.display.specshow(S_db, x_axis="time", y_axis="hz")
plt.colorbar()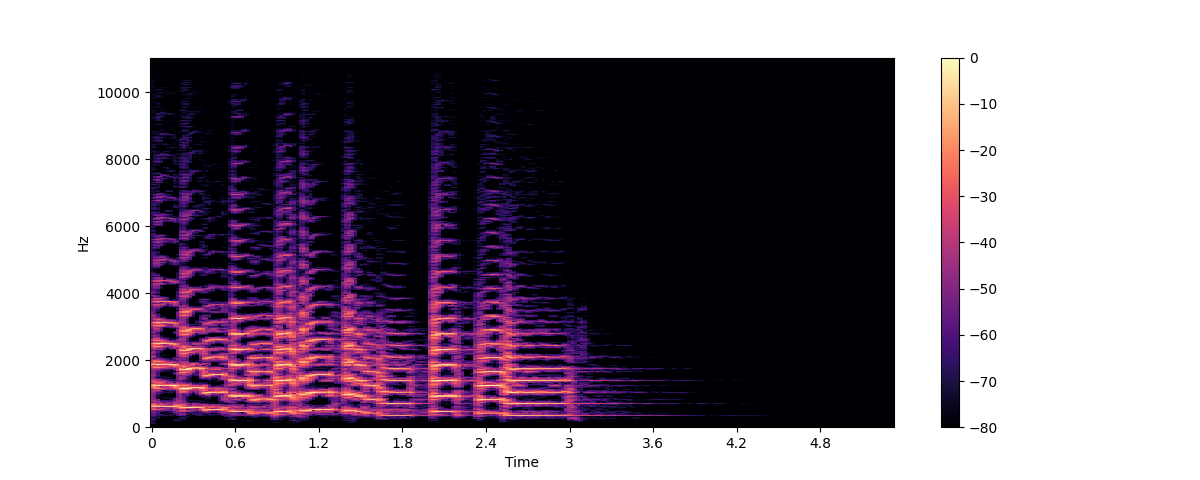

Neste gráfico, o eixo x representa o tempo como na visualização da forma de onda, mas agora o eixo y representa a frequência em Hz. A intensidade da cor dá a amplitude ou potência do componente de frequência em cada ponto no tempo, medida em decibéis (dB).

O espectrograma é criado obtendo trechos curtos do sinal de áudio, geralmente durando alguns milissegundos, e calculando a transformada de Fourier discreta de cada trecho para obter seu espectro de frequência. Os espectros resultantes são colocados em sequência eixo do tempo para criar o espectrograma. Cada fatia vertical nesta imagem corresponde a um único espectro de frequência, como se o gráfico fosse girado. Por padrão, librosa.stft() divide o sinal de áudio em trechos de 2048 amostras, o que dá um bom equilíbrio entre resolução de frequência e resolução de tempo.

Como o espectrograma e a forma de onda são visualizações diferentes dos mesmos dados, é possível transformar o espectrograma de volta na forma de onda original usando a STFT inversa. No entanto, isso requer a informação de fase, além da amplitude. Se o espectograma foi gerado por um modelo de machine learning, geralmente ele contém só as amplitudes. Neste caso, nós podemos usar um algoritmo de reconstrução de fase como o clássico algoritmo de Griffin-Lim ou usar uma rede neural chamada vocoder, que reconstroi a forma de onda partir do espectograma.

Os espectrogramas não são usados apenas para visualização. Muitos modelos de machine learning utilizam espectrogramas como entrada — ao invés de formas de onda — e produzem espectrogramas como saída.

Agora que sabemos o que é um espectrograma e como é feito, vamos dar uma olhada em uma variante dele amplamente usada para o processamento de fala: o espectrograma mel.

Espectrograma Mel

Um espectrograma mel é uma variação do espectrograma que é comumente usada no processamento de fala e tarefas de machine learning. É semelhante a um espectrograma no sentido de que mostra o conteúdo de frequência de um sinal de áudio ao longo do tempo, mas em um eixo de frequência diferente.

Em um espectrograma padrão, o eixo de frequência é linear e é medido em hertz (Hz). No entanto, o sistema auditivo humano é mais sensível a mudanças em frequências mais baixas do que em frequências mais altas, e essa sensibilidade diminui logaritmicamente à medida que a frequência aumenta. A escala mel é uma escala perceptual que aproxima a resposta de frequência não linear do ouvido humano.

Para criar um espectrograma mel, a STFT é usada como antes, dividindo o áudio em segmentos curtos para obter uma sequência de espectros de frequência. Além disso, cada espectro é enviado através de um conjunto de filtros, o chamado banco de filtros mel, para transformar as frequências para a escala mel.

Vamos ver como podemos plotar um espectrograma mel usando a função melspectrogram() da librosa, que realiza todos esses passos para nós:

S = librosa.feature.melspectrogram(y=array, sr=sampling_rate, n_mels=128, fmax=8000)
S_dB = librosa.power_to_db(S, ref=np.max)

plt.figure().set_figwidth(12)
librosa.display.specshow(S_dB, x_axis="time", y_axis="mel", sr=sampling_rate, fmax=8000)
plt.colorbar()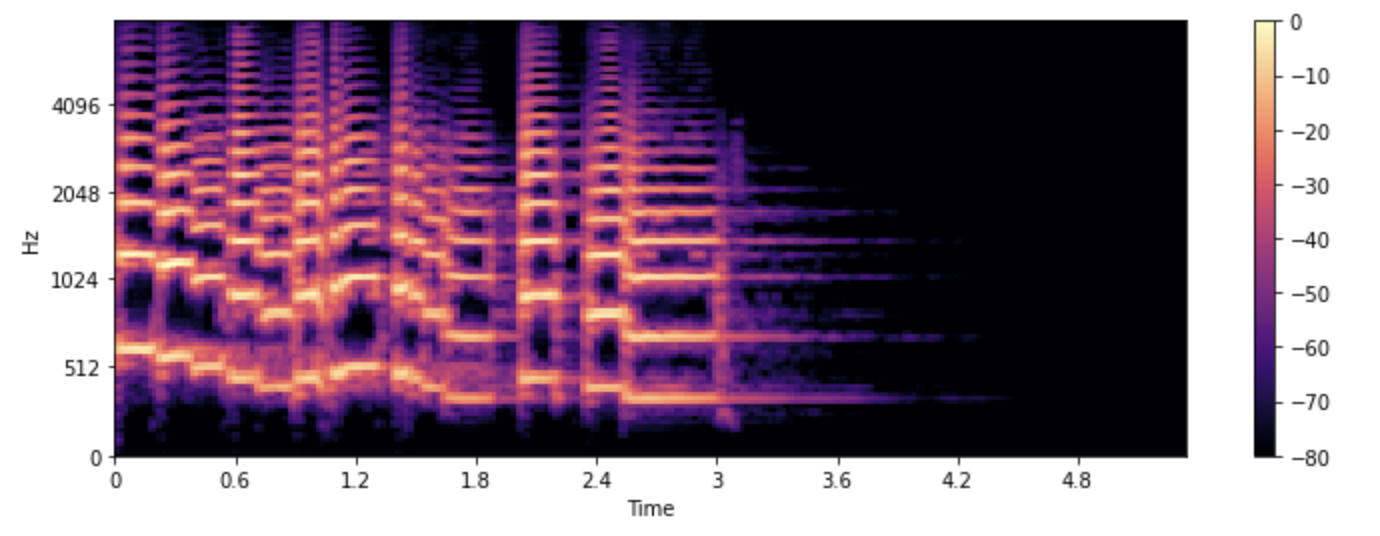

No exemplo acima, n_mels indica o número de bandas mel a serem geradas. As bandas mel definem um conjunto de faixas de frequência que dividem o espectro em componentes perceptualmente significativos, usando um conjunto de filtros cuja forma e espaçamento são escolhidos para imitar a forma como o ouvido humano responde a diferentes frequências. Valores comuns para n_mels são 40 ou 80. fmax indica a frequência mais alta (em Hz) com a qual nos preocupamos.

Assim como com um espectrograma regular, é prática comum expressar a intesidade de cada frequência mel em decibéis. Isso é comumente referido como um espectrograma log-mel, porque a conversão para decibéis envolve uma operação logarítmica. O exemplo acima usou librosa.power_to_db() já que librosa.feature.melspectrogram() cria um espectrograma de potência.

Criar um espectrograma mel é uma operação com perda, pois envolve filtragem do sinal. Converter um espectrograma mel de volta em uma forma de onda é mais difícil do que fazer isso para um espectrograma regular, pois exige a estimação das frequências que foram descartadas. É por isso que modelos de aprendizado de máquina como o vocoder HiFiGAN são necessários para produzir uma forma de onda a partir de um espectrograma mel.

Comparado a um espectrograma padrão, um espectrograma mel pode capturar características mais significativas do sinal de áudio para a percepção humana, tornando-o uma escolha popular em tarefas como reconhecimento de fala, identificação de falante e classificação de gênero musical.

Agora que você sabe como visualizar exemplos de dados de áudio, vá em frente e tente ver como seus sons favoritos parecem. :)