pretty_name: SRSD-Feynman (Easy w/ Dummy Variables)
annotations_creators:
- expert
language_creators:
- expert-generated
language:
- en
license:
- mit
multilinguality:
- monolingual
size_categories:
- 100K<n<1M
source_datasets:
- extended
task_categories:
- tabular-regression
task_ids: []
Dataset Card for SRSD-Feynman (Easy set with Dummy Variables)
Table of Contents
- Table of Contents
- Dataset Description
- Dataset Structure
- Dataset Creation
- Considerations for Using the Data
- Additional Information
Dataset Description
- Homepage:
- Repository: https://github.com/omron-sinicx/srsd-benchmark
- Paper: Rethinking Symbolic Regression Datasets and Benchmarks for Scientific Discovery
- Point of Contact: Yoshitaka Ushiku
Dataset Summary
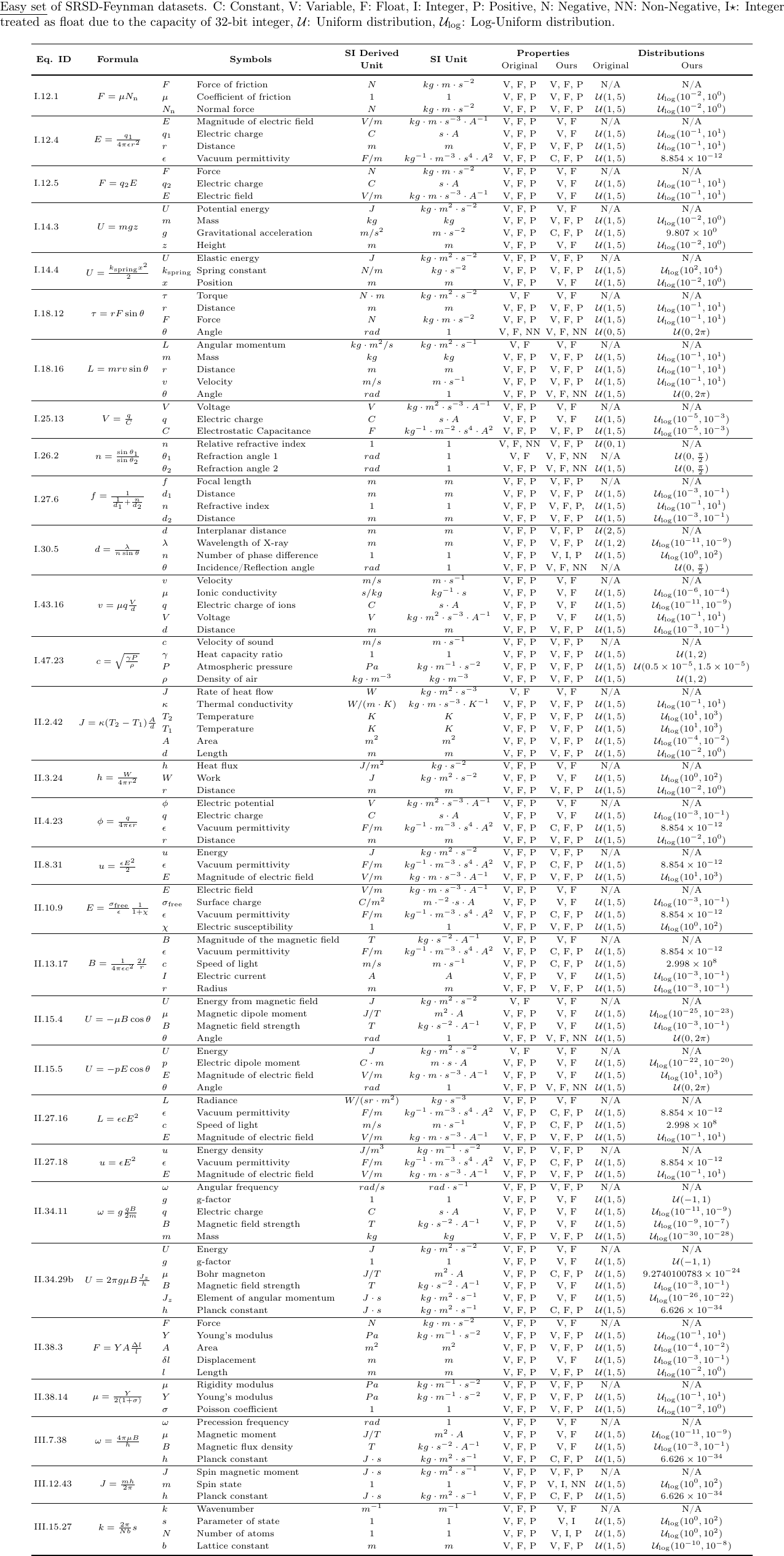
Our SRSD (Feynman) datasets are designed to discuss the performance of Symbolic Regression for Scientific Discovery. We carefully reviewed the properties of each formula and its variables in the Feynman Symbolic Regression Database to design reasonably realistic sampling range of values so that our SRSD datasets can be used for evaluating the potential of SRSD such as whether or not an SR method con (re)discover physical laws from such datasets.
This is the Easy set with dummy variables of our SRSD-Feynman datasets, which consists of the following 30 different physics formulas:
Dummy variables were randomly generated, and symbolic regression models should not use the dummy variables as part of their predictions.
The following datasets contain
1 dummy variable: I.12.1, I.12.4, I.12.5, I.18.12, I.25.13, I.47.23
2 dummy variables: I.14.3, I.18.16, I.43.16, II.3.24, II.8.31, II.10.9, II.13.17, II.15.5, II.27.18, III.7.38, III.12.43
3 dummy variables: I.14.4, I.26.2, I.27.6, I.30.5, II.2.42, II.4.23, II.15.4, II.27.16, II.34.11, II.34.29b, II.38.3, II.38.14, III.15.27
More details of these datasets are provided in the paper and its supplementary material.
Supported Tasks and Leaderboards
Symbolic Regression
Dataset Structure
Data Instances
Tabular data + Ground-truth equation per equation
Tabular data: (num_samples, num_variables+1), where the last (rightmost) column indicate output of the target function for given variables.
Note that the number of variables (num_variables) varies from equation to equation.
Ground-truth equation: pickled symbolic representation (equation with symbols in sympy) of the target function.
Data Fields
For each dataset, we have
- train split (txt file, whitespace as a delimiter)
- val split (txt file, whitespace as a delimiter)
- test split (txt file, whitespace as a delimiter)
- true equation (pickle file for sympy object)
Data Splits
- train: 8,000 samples per equation
- val: 1,000 samples per equation
- test: 1,000 samples per equation
Dataset Creation
Curation Rationale
We chose target equations based on the Feynman Symbolic Regression Database.
Annotations
Annotation process
We significantly revised the sampling range for each variable from the annotations in the Feynman Symbolic Regression Database. First, we checked the properties of each variable and treat physical constants (e.g., light speed, gravitational constant) as constants. Next, variable ranges were defined to correspond to each typical physics experiment to confirm the physical phenomenon for each equation. In cases where a specific experiment is difficult to be assumed, ranges were set within which the corresponding physical phenomenon can be seen. Generally, the ranges are set to be sampled on log scales within their orders as 10^2 in order to take both large and small changes in value as the order changes. Variables such as angles, for which a linear distribution is expected are set to be sampled uniformly. In addition, variables that take a specific sign were set to be sampled within that range.
Who are the annotators?
The main annotators are
- Naoya Chiba (@nchiba)
- Ryo Igarashi (@rigarash)
Personal and Sensitive Information
N/A
Considerations for Using the Data
Social Impact of Dataset
We annotated this dataset, assuming typical physical experiments. The dataset will engage research on symbolic regression for scientific discovery (SRSD) and help researchers discuss the potential of symbolic regression methods towards data-driven scientific discovery.
Discussion of Biases
Our choices of target equations are based on the Feynman Symbolic Regression Database, which are focused on a field of Physics.
Other Known Limitations
Some variables used in our datasets indicate some numbers (counts), which should be treated as integer. Due to the capacity of 32-bit integer, however, we treated some of such variables as float e.g., number of molecules (10^{23} - 10^{25})
Additional Information
Dataset Curators
The main curators are
- Naoya Chiba (@nchiba)
- Ryo Igarashi (@rigarash)
Licensing Information
MIT License
Citation Information
[Preprint]
@article{matsubara2022rethinking,
title={Rethinking Symbolic Regression Datasets and Benchmarks for Scientific Discovery},
author={Matsubara, Yoshitomo and Chiba, Naoya and Igarashi, Ryo and Ushiku, Yoshitaka},
journal={arXiv preprint arXiv:2206.10540},
year={2022}
}
Contributions
Authors:
- Yoshitomo Matsubara (@yoshitomo-matsubara)
- Naoya Chiba (@nchiba)
- Ryo Igarashi (@rigarash)
- Yoshitaka Ushiku (@yushiku)