# 《从零开始学扩散模型》
## 术语表
| 词汇 | 翻译 |
| :---------------------- | :--- |
| Corruption Process | 退化过程 |
| Pipeline | 管线 |
| Timestep | 时间步 |
| Scheduler | 调度器 |
| Gradient Accumulation | 梯度累加 |
| Fine-Tuning | 微调 |
| Guidance | 引导 |
# 目录
## 第一部分 基础知识
### 第一章 扩散模型的原理、发展和应用
#### 1.1 扩散模型的原理
#### 1.2 扩散模型的发展
#### 1.3 扩散模型的应用
### 第二章 HuggingFace介绍与环境准备
#### 2.1 HuggingFace Space
#### 2.2 Transformer 与 diffusers 库
#### 2.3 环境准备
## 第二部分 扩散模型实战
### 第三章 从零开始做扩散模型
#### 3.1 章节概述
#### 3.2 环境准备
#### 3.2.1 环境的创建与导入
#### 3.2.2 数据集测试
#### 3.3 扩散模型-退化过程
#### 3.4 扩散模型训练
#### 3.4.1 Unet模型
#### 3.4.2 开始训练模型
#### 3.5 扩散模型-采样(取样)过程
#### 3.5.1 采样(取样)过程
#### 3.5.2 与DDPM的区别
#### 3.5.3 UNet2DModel模型
#### 3.6 扩散模型-退化过程示例
#### 3.6.1 退化过程
#### 3.6.2 最终的训练目标
#### 3.7 拓展知识
#### 3.7.1 迭代周期(Timestep)的调节
#### 3.7.2 采样(取样)的关键问题
#### 3.8 本章小结
### 第四章 Diffusers实战
#### 4.1 章节概述
#### 4.2 环境准备
#### 4.2.1 安装Diffusers库
#### 4.2.2 Dreambooth-全新的扩散模型
#### 4.2.3 Diffusers核心API
#### 4.3 实战:生成美丽的蝴蝶图片
#### 4.3.1 下载蝴蝶图像集
#### 4.3.2 扩散模型-调度器
#### 4.3.3 定义扩散模型
#### 4.3.4 创建扩散模型训练循环
#### 4.3.5 图像的生成
#### 4.4 拓展知识
#### 4.4.1 将模型上传到Hub上
#### 4.4.2 扩大训练模型的规模
#### 4.5 本章小结
### 第五章 微调和引导
#### 5.1 章节概述
#### 5.2 环境准备
#### 5.3 载入一个预训练过的管线
#### 5.4 DDIM-更快的采样过程
#### 5.5 扩散模型-微调
#### 5.5.1 实战:微调
#### 5.5.2 使用最小化样例脚本微调模型
#### 5.5.3 保存和载入微调过的管线
#### 5.6 扩散模型-引导
#### 5.6.1 实战:引导
#### 5.6.2 CLIP 引导
#### 5.7 分享你的自定义采样训练
#### 5.7.1 环境准备
#### 5.7.2 创建一个以类别为条件的UNet
#### 5.7.3 训练与采样
#### 5.8 本章小结
#### 5.9 实战:创建一个类别条件扩散模型
### 第六章 Stable Diffusion
#### 6.1 章节概述
#### 6.2 环境准备
#### 6.3 从文本生成图像
#### 6.4 Stable Diffusion Pipeline
#### 6.4.1 可变分自编码器(VAE)
#### 6.4.2 分词器(Tokenizer)和文本编码器(Text Encoder)
#### 6.4.3 UNet
#### 6.4.4 调度器(Scheduler)
#### 6.4.5 DIY一个采样循环
#### 6.5 其他管线介绍
#### 6.5.1 Img2Img
#### 6.5.2 In-Painting
#### 6.5.3 Depth2Image
#### 6.5.4 拓展:管理你的模型缓存
#### 6.6 本章小结
### 第七章 DDIM反转
#### 7.1 本章概述
在此篇笔记我们会来探索**反转**,看看它是如何影响采样的,并把它应用到扩散模型的编辑图像功能中去。
##### 你将会学到什么
- DDIM采样是怎么工作的
- 确定性vs随机性采样器
- DDIM反转的理论支撑
- 使用反转来编辑图像
我们开始吧!
#### 7.2 实战:反转
#### 7.2.1 设置
```python
# !pip install -q transformers diffusers accelerate
```
```python
import torch
import requests
import torch.nn as nn
import torch.nn.functional as F
from PIL import Image
from io import BytesIO
from tqdm.auto import tqdm
from matplotlib import pyplot as plt
from torchvision import transforms as tfms
from diffusers import StableDiffusionPipeline, DDIMScheduler
# Useful function for later
def load_image(url, size=None):
response = requests.get(url,timeout=0.2)
img = Image.open(BytesIO(response.content)).convert('RGB')
if size is not None:
img = img.resize(size)
return img
```
```python
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
```
#### 7.2.2 加载一个已训练的管道
```python
# Load a pipeline
pipe = StableDiffusionPipeline.from_pretrained("runwayml/stable-diffusion-v1-5").to(device)
```
```python
# Set up a DDIM scheduler:
pipe.scheduler = DDIMScheduler.from_config(pipe.scheduler.config)
```
```python
# Sample an image to make sure it is all working
prompt = 'Beautiful DSLR Photograph of a penguin on the beach, golden hour'
negative_prompt = 'blurry, ugly, stock photo'
im = pipe(prompt, negative_prompt=negative_prompt).images[0]
im.resize((256, 256)) # resize for convenient viewing
```
#### 7.2.3 DDIM采样
在给定时间 $t$, 带噪图像 $x_t$ 是原始图像($x_0$)与噪声 ($\epsilon$)的叠加。这是在DDIM论文中$x_t$的定义式,我们把它引用到此节里:
$$ x_t = \sqrt{\alpha_t}x_0 + \sqrt{1-\alpha_t}\epsilon $$
$\epsilon$ 是归一方差的高斯噪声
$\alpha_t$ ('alpha')在DDPM论文中也被叫做$\bar{\alpha}$ ('alpha_bar'),被用来定义噪声调度器(scheduler)。在扩散模型中,alpha调度器是被计算出来并被排序存储在`scheduler.alphas_cumprod`中。这有点令人困惑,我理解!我们来把这些值画出来,并在下文中我们会使用DDIM的标注方式。
```python
# Plot 'alpha' (alpha_bar in DDPM language, alphas_cumprod in diffusers for clarity)
timesteps = pipe.scheduler.timesteps.cpu()
alphas = pipe.scheduler.alphas_cumprod[timesteps]
plt.plot(timesteps, alphas, label='alpha_t');
plt.legend();
```
最初(timestep 0 ,图中左侧)是从一个无噪的干净图像开始,$\alpha_t = 1$。当我们到达更高的迭代周期(timesteps),我们得到一个几乎全是噪声的图像,$\alpha_t$也几乎下降到0。
在采样过程,我们从timestep1000的纯噪声开始,慢慢地向timestep0前进。为了计算采样轨迹中的下一时刻($x_{t-1}$ 因为我们是从后向前移动)的值,我们预测噪声($\epsilon_\theta(x_t)$,这就是我们模型的输出),用它来预测出无噪的图片$x_0$。在这之后我们用这个预测结果朝着'$x_t$的方向'方向移动一小步。最终,我们可以加一些带$\sigma_t$系数的额外噪声。这是论文中与上述操作相关的章节内容:

好,我们有了在可控量度噪声下,从$x_t$ 移动到 $x_{t-1}$的公式。今天我们所使用的案例是不需要再额外添加噪声的 - 即完全确定的DDIM采样。我们来看看这些是如何用代码表达的。
```python
# Sample function (regular DDIM)
@torch.no_grad()
def sample(prompt, start_step=0, start_latents=None,
guidance_scale=3.5, num_inference_steps=30,
num_images_per_prompt=1, do_classifier_free_guidance=True,
negative_prompt='', device=device):
# Encode prompt
text_embeddings = pipe._encode_prompt(
prompt, device, num_images_per_prompt, do_classifier_free_guidance, negative_prompt
)
# Set num inference steps
pipe.scheduler.set_timesteps(num_inference_steps, device=device)
# Create a random starting point if we don't have one already
if start_latents is None:
start_latents = torch.randn(1, 4, 64, 64, device=device)
start_latents *= pipe.scheduler.init_noise_sigma
latents = start_latents.clone()
for i in tqdm(range(start_step, num_inference_steps)):
t = pipe.scheduler.timesteps[i]
# expand the latents if we are doing classifier free guidance
latent_model_input = torch.cat([latents] * 2) if do_classifier_free_guidance else latents
latent_model_input = pipe.scheduler.scale_model_input(latent_model_input, t)
# predict the noise residual
noise_pred = pipe.unet(latent_model_input, t, encoder_hidden_states=text_embeddings).sample
# perform guidance
if do_classifier_free_guidance:
noise_pred_uncond, noise_pred_text = noise_pred.chunk(2)
noise_pred = noise_pred_uncond + guidance_scale * (noise_pred_text - noise_pred_uncond)
# Normally we'd rely on the scheduler to handle the update step:
# latents = pipe.scheduler.step(noise_pred, t, latents).prev_sample
# Instead, let's do it ourselves:
prev_t = max(1, t.item() - (1000//num_inference_steps)) # t-1
alpha_t = pipe.scheduler.alphas_cumprod[t.item()]
alpha_t_prev = pipe.scheduler.alphas_cumprod[prev_t]
predicted_x0 = (latents - (1-alpha_t).sqrt()*noise_pred) / alpha_t.sqrt()
direction_pointing_to_xt = (1-alpha_t_prev).sqrt()*noise_pred
latents = alpha_t_prev.sqrt()*predicted_x0 + direction_pointing_to_xt
# Post-processing
images = pipe.decode_latents(latents)
images = pipe.numpy_to_pil(images)
return images
```
```python
# Test our sampling function by generating an image
sample('Watercolor painting of a beach sunset', negative_prompt=negative_prompt, num_inference_steps=50)[0].resize((256, 256))
```
看看你是否能把这些代码和论文中的公式对应起来。注意$\sigma$=0是因为我们只注意 无-额外-噪声 的场景,所以我们略去了公式中的那部分。
#### 7.2.4 反转
反转的目标就是'颠倒'取样的过程。我们想最终得到一个带噪的隐式(latent),如果把它作为我们正常取样过程的起始点,结果将生成一副原图像。
这里我们先加载一个原始图像,当然你也可以生成一副图像来代替。
```python
# https://www.pexels.com/photo/a-beagle-on-green-grass-field-8306128/
input_image = load_image('https://images.pexels.com/photos/8306128/pexels-photo-8306128.jpeg', size=(512, 512))
input_image
```
我们可以用包含随意分类指引(classifier-free-guidance)的prompt来做反转操作,输入一个图片的描述:
```python
input_image_prompt = "Photograph of a puppy on the grass"
```
接下来我们来把这个PIL图像变成一些列隐式,它们会被用来当作反转的起点:
```python
# encode with VAE
with torch.no_grad(): latent = pipe.vae.encode(tfms.functional.to_tensor(input_image).unsqueeze(0).to(device)*2-1)
l = 0.18215 * latent.latent_dist.sample()
```
好了,到有趣的部分了。这个函数看起来和上面的取样函数很像,但我们在timesteps上是在向相反的方向移动,从t=0开始,向越来越多的噪声前进。代替更新隐式时噪声会越来越少,我们估计所预测出的噪声,用它来撤回一步更新操作,把它们从t移动到t+1。
```python
## Inversion
@torch.no_grad()
def invert(start_latents, prompt, guidance_scale=3.5, num_inference_steps=80,
num_images_per_prompt=1, do_classifier_free_guidance=True,
negative_prompt='', device=device):
# Encode prompt
text_embeddings = pipe._encode_prompt(
prompt, device, num_images_per_prompt, do_classifier_free_guidance, negative_prompt
)
# latents are now the specified start latents
latents = start_latents.clone()
# We'll keep a list of the inverted latents as the process goes on
intermediate_latents = []
# Set num inference steps
pipe.scheduler.set_timesteps(num_inference_steps, device=device)
# Reversed timesteps <<<<<<<<<<<<<<<<<<<<
timesteps = reversed(pipe.scheduler.timesteps)
for i in tqdm(range(1, num_inference_steps), total=num_inference_steps-1):
# We'll skip the final iteration
if i >= num_inference_steps - 1: continue
t = timesteps[i]
# expand the latents if we are doing classifier free guidance
latent_model_input = torch.cat([latents] * 2) if do_classifier_free_guidance else latents
latent_model_input = pipe.scheduler.scale_model_input(latent_model_input, t)
# predict the noise residual
noise_pred = pipe.unet(latent_model_input, t, encoder_hidden_states=text_embeddings).sample
# perform guidance
if do_classifier_free_guidance:
noise_pred_uncond, noise_pred_text = noise_pred.chunk(2)
noise_pred = noise_pred_uncond + guidance_scale * (noise_pred_text - noise_pred_uncond)
current_t = max(0, t.item() - (1000//num_inference_steps))#t
next_t = t # min(999, t.item() + (1000//num_inference_steps)) # t+1
alpha_t = pipe.scheduler.alphas_cumprod[current_t]
alpha_t_next = pipe.scheduler.alphas_cumprod[next_t]
# Inverted update step (re-arranging the update step to get x(t) (new latents) as a function of x(t-1) (current latents)
latents = (latents - (1-alpha_t).sqrt()*noise_pred)*(alpha_t_next.sqrt()/alpha_t.sqrt()) + (1-alpha_t_next).sqrt()*noise_pred
# Store
intermediate_latents.append(latents)
return torch.cat(intermediate_latents)
```
把它在小狗图片的隐式表达上运行,我们可以在反转的中间过程得到一系列的隐式:
```python
inverted_latents = invert(l, input_image_prompt,num_inference_steps=50)
inverted_latents.shape
```
0%| | 0/49 [00:00
Your browser does not support the audio element.
这里,`rate`参数明确了音频的 _采样率_ ;过会儿我们会再深入了解它。同时你也会注意到pipeline也返回了几样其他的东西。这发生了什么?我们来仔细看看这两个输出。
第一项是一个数据数组,代表生成的音频:
```python
# The audio array:
output.audios[0].shape
```
(1, 130560)
第二项看起来像是灰度图:
```python
# The output image (spectrogram):
output.images[0].size
```
(256, 256)
这给了我们一个提示,关于这个pipeline是如何工作的。音频不是直接被扩散模型生成 - 而是,这个pipeline有着与在第一单元看到的无条件图像生成pipelines类似的2D Unet结构 [Unit 1](https://github.com/huggingface/diffusion-models-class/tree/main/unit1) 用它来生成频谱,之后再在后处理中把它变化为最终的音频。
此pipe中有额外的组件来处理这个变化,我们可以通过`pipe.mel`来进行:
```python
pipe.mel
```
Mel {
"_class_name": "Mel",
"_diffusers_version": "0.12.0.dev0",
"hop_length": 512,
"n_fft": 2048,
"n_iter": 32,
"sample_rate": 22050,
"top_db": 80,
"x_res": 256,
"y_res": 256
}
#### 8.2.3 从音频到频谱的转换
音频的'波形'从时间上表现出了源音频 - 比如,这可能是接收自麦克风的电信号。从这种'时域'的表达方式上做处理会有些棘手,所以有种更普遍的做法把它转换成其他形式,通常把这叫做频谱。频谱直接展示出在不同频率(y轴)与时间(x轴)上的剧烈程度。
```python
# Calculate and show a spectrogram for our generated audio sample using torchaudio
spec_transform = AT.Spectrogram(power=2)
spectrogram = spec_transform(torch.tensor(output.audios[0]))
print(spectrogram.min(), spectrogram.max())
log_spectrogram = spectrogram.log()
plt.imshow(log_spectrogram[0], cmap='gray');
```
tensor(0.) tensor(6.0842)

我们刚刚做好的这个频谱取值范围在0.0000000000001到1之间,其中大部分内容都接近取值下限。这对于可视化与建模并不理想 - 实际上我们需要对这些值取log来得到一个可以看到更多细节的灰度图。同样也因此,我们特别使用一种专门的梅尔频谱(Mel spectrogram),这是一种通过对不同频率成分做一些变化,专门设计的一种符合人耳感知特性而利于提取重要信息的方式。
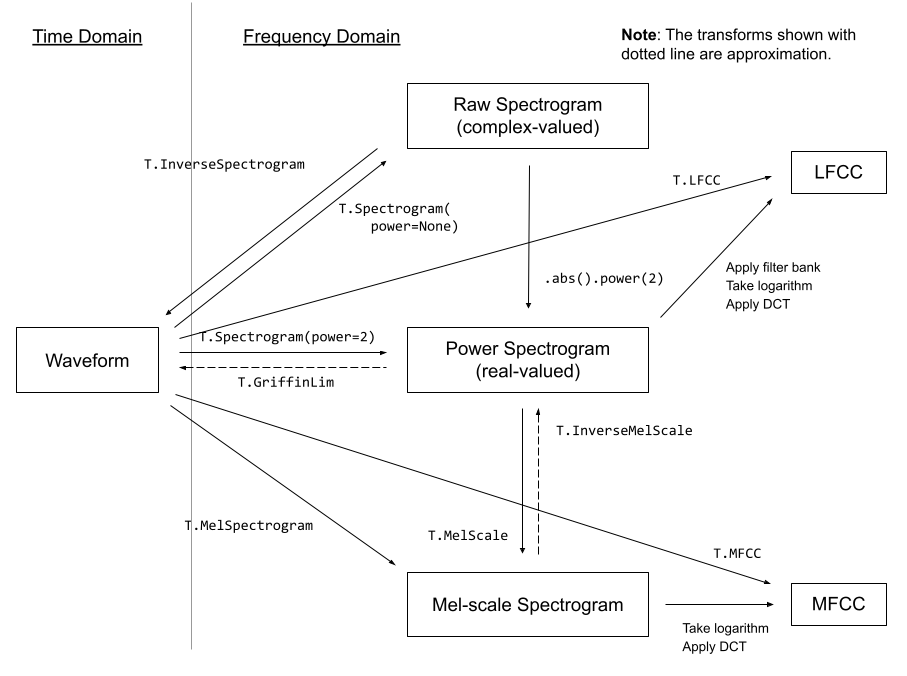
_一些来自 [torchaudio docs](https://pytorch.org/audio/stable/transforms.html)的音频转换方法_
幸运的是,我们并不需要太过于担心这些变换方法 - pipeline中的`mel`功能会为我们处理这些细节。这样操作,我们就能把频谱图像转换成音频:
```python
a = pipe.mel.image_to_audio(output.images[0])
a.shape
```
(130560,)
我们可以先读出源音频数据然后调用 `audio_slice_to_image()`函数来把音频数组数据转化为频谱图片。更长的片段会被自动切片为能够正常输出 256x256 频谱图片的长度。
```python
pipe.mel.load_audio(raw_audio=a)
im = pipe.mel.audio_slice_to_image(0)
im
```

音频被表现为一串很长的数字数组。要把它播放出来的话,我们还需要一个关键信息:采样率。我们要用到多少个采样点(单个的数值),才能够播放出单位秒的音频呢?
我们可以在pipeline中这样来看使用的采样率:
```python
sample_rate_pipeline = pipe.mel.get_sample_rate()
sample_rate_pipeline
```
22050
如果我们故意把采样率设置错误,可以得到一个可能被加速或慢放的音频:
```python
display(Audio(output.audios[0], rate=44100)) # 2x speed
```
#### 8.2.4 微调管道
现在我们已经大致理解了这个pipeline是怎么工作的,现在来在一些新音频数据上对它进行微调!
这个数据集是不同类别的音频片段集合,我们可以从hub上这样加载它:
```python
from datasets import load_dataset
dataset = load_dataset('lewtun/music_genres', split='train')
dataset
```
你可以使用下面的代码来看看在数据集中各类别样本的占比:
```python
for g in list(set(dataset['genre'])):
print(g, sum(x==g for x in dataset['genre']))
```
Pop 945
Blues 58
Punk 2582
Old-Time / Historic 408
Experimental 1800
Folk 1214
Electronic 3071
Spoken 94
Classical 495
Country 142
Instrumental 1044
Chiptune / Glitch 1181
International 814
Ambient Electronic 796
Jazz 306
Soul-RnB 94
Hip-Hop 1757
Easy Listening 13
Rock 3095
这个数据集把音频存储为数组:
```python
audio_array = dataset[0]['audio']['array']
sample_rate_dataset = dataset[0]['audio']['sampling_rate']
print('Audio array shape:', audio_array.shape)
print('Sample rate:', sample_rate_dataset)
display(Audio(audio_array, rate=sample_rate_dataset))
```
Audio array shape: (1323119,)
Sample rate: 44100
注意这条音频的采样率会更高 - 如果我们想用手头的这个pipeline,需要对它'重采样'来匹配。这个片段也比pipeline所预设的长度更长。幸运的是,当我们使用`pipe.mel`在加载音频时,会自动把它切片成更短的片区。
```python
a = dataset[0]['audio']['array'] # Get the audio array
pipe.mel.load_audio(raw_audio=a) # Load it with pipe.mel
pipe.mel.audio_slice_to_image(0) # View the first 'slice' as a spectrogram
```

我们要记得去调整采样率,因为此数据集的数据在每秒中有着多两倍的数据点。
```python
sample_rate_dataset = dataset[0]['audio']['sampling_rate']
sample_rate_dataset
```
44100
这里我们用torchaudio's transforms(import as AT)来做音频的重采样,pipe中的`mel`把音频转换为图像,torchvision's transforms(导入为IT)来把图片转换为tensors。这个函数可以把音频片段转换为频谱tensor供训练使用:
```python
resampler = AT.Resample(sample_rate_dataset, sample_rate_pipeline, dtype=torch.float32)
to_t = IT.ToTensor()
def to_image(audio_array):
audio_tensor = torch.tensor(audio_array).to(torch.float32)
audio_tensor = resampler(audio_tensor)
pipe.mel.load_audio(raw_audio=np.array(audio_tensor))
num_slices = pipe.mel.get_number_of_slices()
slice_idx = random.randint(0, num_slices-1) # Pic a random slice each time (excluding the last short slice)
im = pipe.mel.audio_slice_to_image(slice_idx)
return im
```
来使用我们的`to_image()`函数来组成我们特定的整理函数(collate function)来把数据集转换到dataloader中来训练模型。整理函数定义了如何把一批来自数据集的样例变换为最终的训练用数据。在这个例子中我们把每个音频转换为频谱图像再把他们的tensors堆叠起来:
```python
def collate_fn(examples):
# to image -> to tensor -> rescale to (-1, 1) -> stack into batch
audio_ims = [to_t(to_image(x['audio']['array']))*2-1 for x in examples]
return torch.stack(audio_ims)
# Create a dataset with only the 'Chiptune / Glitch' genre of songs
batch_size=4 # 4 on colab, 12 on A100
chosen_genre = 'Electronic' # <<< Try training on different genres <<<
indexes = [i for i, g in enumerate(dataset['genre']) if g == chosen_genre]
filtered_dataset = dataset.select(indexes)
dl = torch.utils.data.DataLoader(filtered_dataset.shuffle(), batch_size=batch_size, collate_fn=collate_fn, shuffle=True)
batch = next(iter(dl))
print(batch.shape)
```
torch.Size([4, 1, 256, 256])
**留心: 你可能要用一个更小的batchsize(比如4)除非你有足够的显存可用**
#### 8.2.5 循环训练
这是一个在dataloader中读取数据的简洁训练循环,用几个周期来微调pipeline的UNet网络。你可以跳过此块,直接使用下一块代码来加载pipeline。
```python
epochs = 3
lr = 1e-4
pipe.unet.train()
pipe.scheduler.set_timesteps(1000)
optimizer = torch.optim.AdamW(pipe.unet.parameters(), lr=lr)
for epoch in range(epochs):
for step, batch in tqdm(enumerate(dl), total=len(dl)):
# Prepare the input images
clean_images = batch.to(device)
bs = clean_images.shape[0]
# Sample a random timestep for each image
timesteps = torch.randint(
0, pipe.scheduler.num_train_timesteps, (bs,), device=clean_images.device
).long()
# Add noise to the clean images according to the noise magnitude at each timestep
noise = torch.randn(clean_images.shape).to(clean_images.device)
noisy_images = pipe.scheduler.add_noise(clean_images, noise, timesteps)
# Get the model prediction
noise_pred = pipe.unet(noisy_images, timesteps, return_dict=False)[0]
# Calculate the loss
loss = F.mse_loss(noise_pred, noise)
loss.backward(loss)
# Update the model parameters with the optimizer
optimizer.step()
optimizer.zero_grad()
```
```python
# OR: Load the version I trained earlier:
pipe = DiffusionPipeline.from_pretrained("johnowhitaker/Electronic_test").to(device)
```
Downloading: 0%| | 0.00/282 [00:00
Your browser does not support the audio element.
```python
# Make a longer sample by passing in a starting noise tensor with a different shape
noise = torch.randn(1, 1, pipe.unet.sample_size[0],pipe.unet.sample_size[1]*4).to(device)
output = pipe(noise=noise)
display(output.images[0])
display(Audio(output.audios[0], rate=22050))
```
0%| | 0/1000 [00:00
Your browser does not support the audio element.
这个输出听起来绝不是最好的,但这是一个开始 :)探索一下调整学习率和迭代周期,并在Discord上分享你的最佳结果,我们就可以来一起进步了!
一些需要考虑的事情
- 我们使用的是256像素点的方形频谱图片,这会限制住我们的batchsize。你能够从128x128的频谱中恢复出质量足够好的音频吗?
- 为了替代随机图像增强,我们每次挑选不同的音频片段,但这种做法在训练迭代的后期是否可以用其他增强方式再优化一下?
- 我们有什么其他办法可以用它来生成更长的音频?也许你可以先生成开头的5s音频然后再用类似图像修复的思路接着卡开头片段来继续生成后续内容...
- 扩散模型生成的内容与图像到图像的生成有什么相同之处?
#### 8.3 将模型上传到Hub上
当你对你的模型足够满意了,你就可以把它保存下来并上传到hub上给他人来共享:
```python
from huggingface_hub import get_full_repo_name, HfApi, create_repo, ModelCard
```
```python
# Pick a name for the model
model_name = "audio-diffusion-electronic"
hub_model_id = get_full_repo_name(model_name)
```
```python
# Save the pipeline locally
pipe.save_pretrained(model_name)
```
```python
# Inspect the folder contents
!ls {model_name}
```
mel model_index.json scheduler unet
```python
# Create a repository
create_repo(hub_model_id)
```
```python
# Upload the files
api = HfApi()
api.upload_folder(
folder_path=f"{model_name}/scheduler", path_in_repo="scheduler", repo_id=hub_model_id
)
api.upload_folder(
folder_path=f"{model_name}/mel", path_in_repo="mel", repo_id=hub_model_id
)
api.upload_folder(folder_path=f"{model_name}/unet", path_in_repo="unet", repo_id=hub_model_id)
api.upload_file(
path_or_fileobj=f"{model_name}/model_index.json",
path_in_repo="model_index.json",
repo_id=hub_model_id,
)
```
```python
# Push a model card
content = f"""
---
license: mit
tags:
- pytorch
- diffusers
- unconditional-audio-generation
- diffusion-models-class
---
# Model Card for Unit 4 of the [Diffusion Models Class 🧨](https://github.com/huggingface/diffusion-models-class)
This model is a diffusion model for unconditional audio generation of music in the genre {chosen_genre}
## Usage
```python
from IPython.display import Audio
from diffusers import DiffusionPipeline
pipe = DiffusionPipeline.from_pretrained("{hub_model_id}")
output = pipe()
display(output.images[0])
display(Audio(output.audios[0], rate=pipe.mel.get_sample_rate()))"""
```
```
card = ModelCard(content)
card.push_to_hub(hub_model_id)
```
#### 8.4 本章小结
希望这片笔记让你浅尝到音频生成的潜力。请再留意下此单元在介绍中的一些参考链接,去看一些更酷炫的方法和它们所创造的惊艳内容!
### 第九章 ControlNet和LoRa
#### 9.1 ControlNet
#### 9.2 LoRa
## 附录 精美图像集展示